D dx (x2) = 1 x2 ×2x = 2 x. If y = mx + 4 is a tangent to both the parabolas:

Picture Math Olympiad Ap Calculus Calculus
Then k( 1 x + 1 y) = logx +logy.
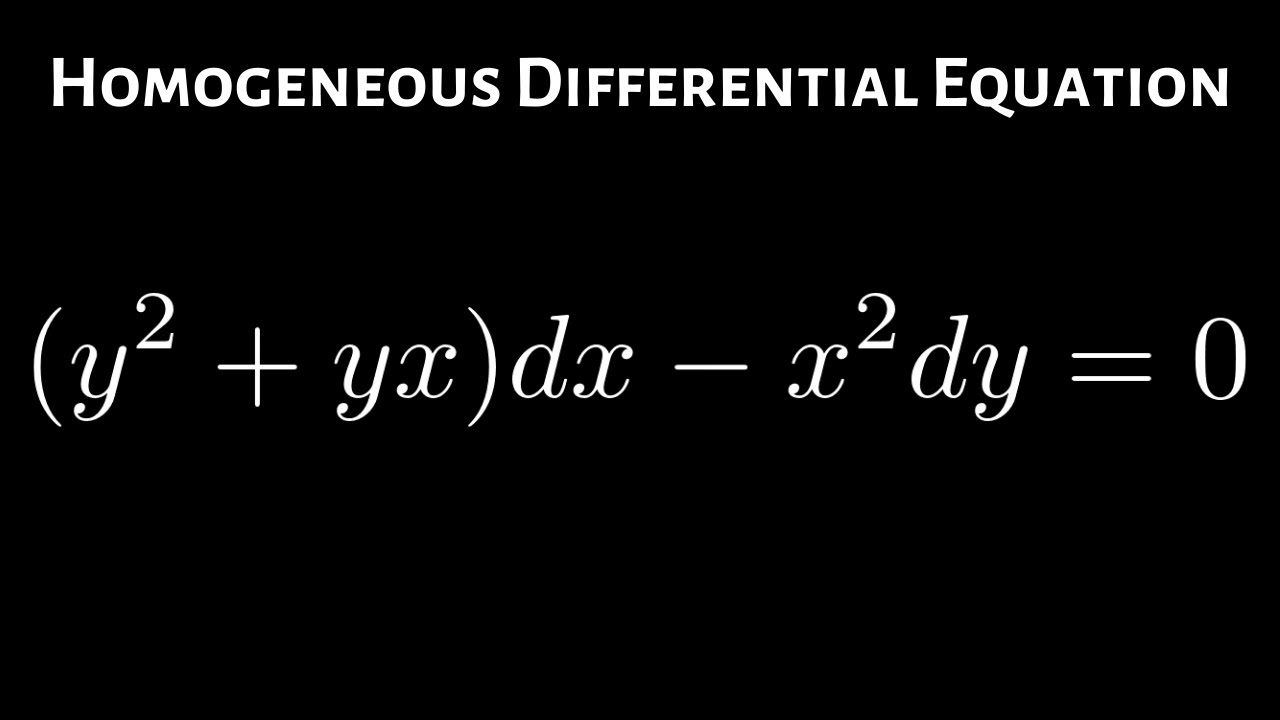
Y log x=(x-y). Let v = x log x. If y = sin (log e x), then x 2 d 2 y/dx 2 + x dy/dx is equal to: ⇒ logxy x+y xy = logyz y+z yz = logzx z+x zx.
(1) k( 1 y + 1 z) = logy + logz. Y = log(x2) ⇒ dy dx = 1 x2. Log b (x y) = y ∙ log b (x) for example:
In the equation y = log b x, the value y is the answer to the question to what power must b be raised, in order to yield x?. Find #dy/dx#of #y=x^logx +(log x)^x#? Using y axis part as mirror draw the image of right handed side of graph inq2 and q3.
The product rule can be used for fast multiplication calculation using addition operation. Tiger was unable to solve based on your input y=log5x logarithms not yet implemented. Let u = x 2.
If y = log cos x sin x, then dy/dx is equal to: It is possible to imagine a situation where this could be useful.$\endgroup$. What is the lewis structure for co2?
The logarithm of the division of x and y is the difference of logarithm of x and logarithm of y. 1 answer epsilon may 24, 2018 explanation: Log only has product rule and quotient rule and there is no rule for addition/ subtraction of 2 numbers.
Are solved by group of students and teacher of ca foundation, which is also the largest student community of ca foundation. If y = 3 cos (log x) + 4 sin (log x), show that: ⇒ logx +logy 1 x + 1 y = logy + logz 1 y + 1 z = logz +logx 1 z + 1 x = k say.
Log b (x ∙ y) = log b (x) + log b (y). 2.now neglect the graph in q2 and q3. Putting the value of function y = log a x in the above equation, we get.
Please see the image file to explanation. 1.draw the graph of y= log x which originated from negative infinity in q2 and having y axis as asymptote and increases rapidly having intercept of +1 unit on y axis. $\begingroup$you could expand using the taylor series.$\endgroup$.
Apr 2 '13 at 11:04. If the answer is not available please wait for a while and a community member will probably answer this soon. 'm' is the difference between the highest and the least values of n.
I would like some help with proving the following theorem, which i found in some lectures notes on analysis: What is the lewis structure for hcn? V y=log5x program execution terminated tiger was not able to solve for your input:y=log5x submit your.
This make sense because 0 = log a 1 0 = log. Log 10 (2 8) = 8∙ log. First we take the increment or small change in the function:
Log b (3 ∙ 7) = log b (3) + log b (7). 0$ then $\log(xy) = \log x + \log y$. ×y = log(4x) ⇒ 4x = 10y ⇒ x = 410y.
The logarithm of x raised to the power of y is y times the logarithm of x. How do i determine the molecular shape of a molecule? Using the law of logs then differentiate.
X^2d^2y/dx^2 + xdy/dx + y = 0. Log v = log x log x. A family is comparing different car seats.
The graphs of y = log 2 x, y = log 2 x, y = log 3 x, y = log 3 x, and y = log 5 x y = log 5 x are the shape we expect from a logarithmic function where a > 1. Askednov 9, 2018in mathematicsby samantha(38.9kpoints) continuity and differntiability. Lo g (x + y) = 2 x y on differentiating both sides w.r.t x, we get (x + y 1 ) (1 + d x d y ) = 2 (x d x d y + y) ⇒ d x d y = 2 x 2 + 2 x y − 1 1 − 2 x y − 2 y 2 at x = 0, y = 1 (from lo g x + y = 2 x y) now, at x = 0, y ′ (0) = − 1.
Y = logx2 = 2logx. Y = f ( x) = log a x. Given y = x 2 + x log x.
Reminder ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯∣∣ ∣ 2 2logxn = nlogx2 2 ∣∣ ∣ −−−−−−−−−−−−−−−−−−. A unique platform where students can interact with teachers/experts/students to get solutions to their queries. The log of a quotient is the difference of the logs.
Xylogxy x +y = yzlogyz y +z = zxlogzx z +x. The logarithm of a multiplication of x and y is the sum of logarithm of x and logarithm of y. We notice that for each function the graph contains the point (1, 0).
If $y\ne 0$, we can rewrite $x+y$ as $y(1+\frac{x}{y})$, and then get $\log(x+y)=\log y +\log\left(1+\frac{x}{y}\right)$. Take log on both sides. ⇒ dy dx = 2 × 1 x = 2 x.
The questions and answers of logx logy=log(x y),y can be expressed as ?

Pin By Achmad Yanu On Math Magic Studying Math Learning Mathematics Gcse Math

Pin On Rumus Matematika Kk Farrel

Rules Of Logarithmic Equations Math Quotient Rule Product Rule

Resolved Logarithmic Equations And Systems And Demostrations Properties Of Logarithms And Change Of Studying Math Learning Mathematics Physics And Mathematics

Digital Study Center Basic Rules Of Logarithm Math Lessons Physics Formulas Basic

Mathematics Studying Math Math Formula Chart Learning Mathematics

Algebra Formulas - Math Algebraic Expression - For Class 91011 Ssc Download In Pdf - Experhap Algebra Formulas Algebraic Expressions Math Formulas

Rbse Solutions For Class 12 Maths Chapter 12 Differential Equation Ex 126 Httpswwwrbsesolutionscomclass-12-maths Class 12 Maths 12th Maths Studying Math

Visualizingmath Log Rules Mathematics Science Nature

Logarithm Rules Dodi_a111 Dodi Dodi Dodi Matematika Oke Log Rules Math 8 Math

Algebra Dance Funny Graph Figures Math Equation - Yx Yx2 Yx3 Ysinx Ycosx Ytanx Ycotx Y1x Y-1x Yx Y-x Y-x Ylogx Prod Funny Dance Algebra

Pin By Joe Pruitt On Logarithms Studying Math Math Methods Algebra

Resolved Logarithmic Equations And Systems And Demostrations Properties Of Logarithms And Change Of Va Studying Math Learning Mathematics Systems Of Equations

Pin On Rbse Solutions For Class 12 Maths
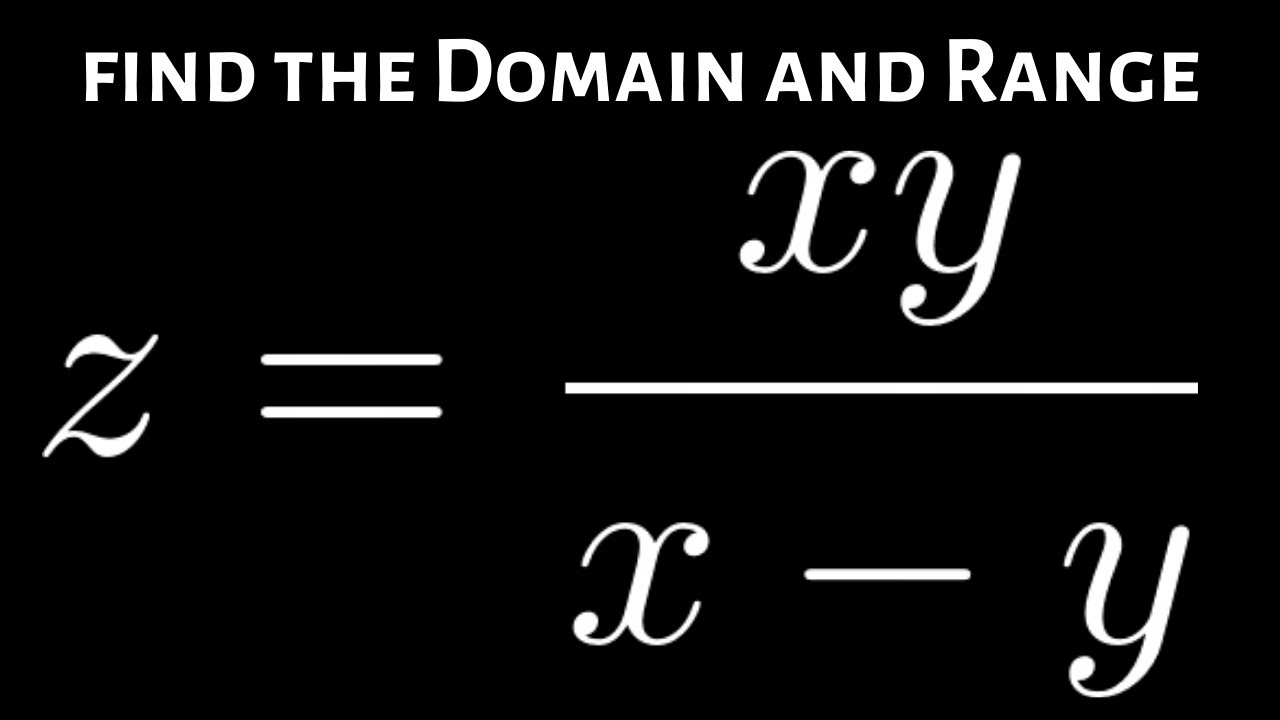
How To Find The Domain And Range Of Z Xyx - Y Math Videos Domain Calculus

American High School Online Home School - Start Your Own Virtual School Start In 2020 Studying Math Mathematics Education Learning Math

How To Find The Domain And Range Of Fx Y Lnxy - 2 Math Videos Fx Domain
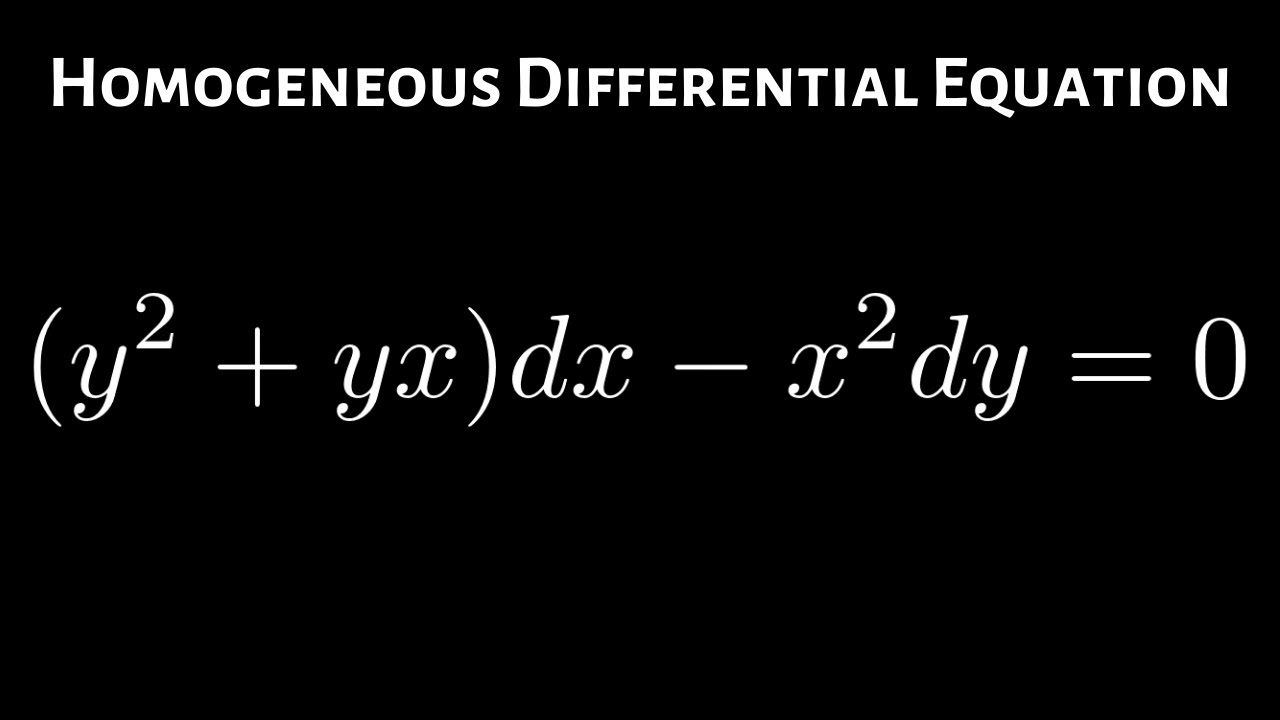
Homogeneous Differential Equation Y2 Yxdx - X2dy 0 Differential Equations Math Videos How To Become


Posting Komentar